模型思维(11)--路径依赖
上一篇我们讲到随机走动,这一篇我们将继续延伸这个话题。如果每次的行动与之前的行为结果相关,我们就可以得到路径依赖模型。在生活中,我们穿的衣服、读的书、看的电影,以及任何需要我们付出时间的活动,都可以应用路径依赖来分析。
波利亚过程
我们利用波利亚过程来刻画正反馈的效应。这里我们依旧使用从瓮里取白球和灰球的实验。一只瓮里面装着一个白球和一个灰球。每一周期,都随机抽取出一个球并将这个球与和它颜色相同的另一个球一起放回到瓮中。抽取出来的球的颜色表示结果。
波利亚过程可以用来刻画各种社会和经济现象。一个人选择学习打网球,还是打篮球,可能取决于其他人的选择。如果更多的朋友选择学习打网球,那么这个人就更有可能也选择学习打网球,因为这会增加他找到伙伴打比赛的机会。与此类似,一个人决定购买什么类型的软件、学习哪种语言或购买哪款智能手机,也可能取决于他的朋友以前做出的选择。
波利亚过程可以得到两个性质:
- 具有相同数量的白色结果的任何序列都会以相同的概率发生 P(GWWW) = P(WWWG)
- 白球和灰球的每个分布都以相同的概率发生 P(白球出现1次) = P(白球出现n次)
第二个性质就可以说明极端情况的可能性,白球只出现1%和白球出现50%的可能性是一样的。我们可以通过实验这个结果,初始只有两个球,之后进行100次抽取,统计其中白球的数量。将此实验重复10000次,理论上每一种白球的分布出现次数在100次左右。结果如图,发现每一种可能都是在100次的上下波动。
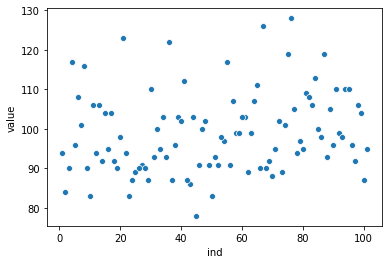
所以这就带来了一个问题。我们可以把消费者对于商品的选择看作波利亚过程,所以消费者对于产品的某些性质的长期偏好可能是随机的。我们利用之前的经验想获得同样的结果是不可能的,因为出现任意的结果概率是相同的。一种解决办法是在将一些特性放在生产链的最后,当发现消费者出现了某种偏好后,根据其想法改变生产线。
均衡过程
均衡过程去波利亚过程的假设是相反的,可以用来刻画负反馈过程。在抽取某种颜色的球后,加入一个相反颜色的球。长远来看,瓮收敛为每种颜色球比例都相同。
均衡过程可以用来刻画有趋向平等分配压力的决策或行动序列。有两个孩子的父母可能会尝试给每个孩子分配相同的时间。与一个孩子共度了一个下午之后,父母会产生与另一个孩子共度更多时光的愿望。
平衡过程甚至可以用来对努力实现公平的组织行为建模。例如奥运会的举办地点,国际奥委会希望世界各地都能举办奥运会。所以在举办地点上,每年都在各大洲之间轮换。
路径依赖的应用
在现实世界中,路径依赖可能不会像波利亚过程那样极端。然而,我们还是可以从模型中推断出当行为具有很大的社会性成分时,几乎任何事情都有可能发生。在任何时候,只要人们在一组固定的备选项中进行选择,而且他们的选择依赖于其他人先前做出的选择时,就会出现这种情况。这样的例子包括在选举中投谁的票、要看哪一部电影,以及购买哪一种技术等。
如果我们在构建一个新产品时,得出其结果取决于路径的早期部分,那么尽早进入、进行干预可能是一个不错的策略。这个模型为企业尽早将产品推向市场或提供大幅度的折扣以便尽可能多地吸引早期用户提供了合理的解释。