模型思维(10)--随机走动
我们在这篇研究随机走动(random walk)。想象有一个点,每次可以随机的前进或退后一步,之后记录其与原点的距离。看似这个过程很简单,却可以利用其结论分析一些时间序列,例如销售额,股票价格等等。随机走动最初是用在研究物理学中液体和气体中粒子的运动,后来发现在生活中的很多现象也符合随机走动。
伯努利瓮模型
我们这里首先利用伯努利瓮模型研究随机走动。假设有一个装了灰球和白球的瓮,其中灰球有G个,白球W个。每一次从中取出一个球,记录抽取出来球的颜色。在下一次抽取之前,球要放回瓮中。每次抽到灰球的概率是 $P = \frac{G}{G + W}$。在抽取N次的情况下,可以计算出抽取出来的灰球的期望数量是$N_G$, 其标准差是 $\sigma_{N_G}$
$$N_G = N \times P$$
$$\sigma_{N_G} = \sqrt{N \times P \ times (1-P)}$$
出现连续n次都是灰球的概率是 $P^n$, 一般情况下出现的可能性很小。假设一个篮球运动员在投三分是有一定概率的,即使一次投中的概率是70%,连续10次投中的概率也就只有3%左右的可能性。
这个模型很简单,也是随机走动模型的基础。
随机走动模型
我们在伯努利瓮模型中,将过去的模型保存下来。我们将初始值设成0,当取出一个白球时,将总数加1,当取出一个灰球时,总数减1。模型在任何时候的状态都等于先前结果的总和,也就是抽取出来的白球总数减去抽取出来的灰球总数的值。
$$V_{t+1} = $V_{t} + R(-1, 1)$$
其中,$V_t$表示时间t上的随机游走值,$V_0=0$,R(1,-1)是一个可能等于1或-1的随机变量。在任何时间段内,这个随机游走的期望值都等于零,且标准差为$\sqrt{t}$,其中的$t$等于周期数。
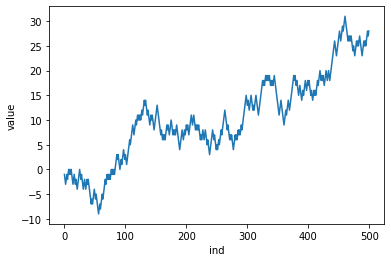
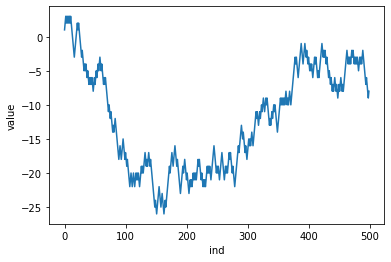
这里是两张P=0.5,t=500的图。简单随机游走既是周期性的(会无限次地返回零点),又是无界性的(会超过任何正的或负的阈值)。如果等待足够长的时间,随机游走会高于正的1万、低于负的100万,也会无限次地穿过零线。此外,返回零点所需的步数分布满足幂律。在大多数时候,返回零只需几步。所有游走中,有一半是两步返回的,然而有些游走需要很长时间才能返回。第二张图就可以看出在负值经历很长时间后才返回零点。
幂律分布结果还有一个意想不到的应用领域。如果我们将企业的销售水平或员工规模建模为随机游走,那么企业的生命周期就会成为一个幂律分布。更准确地说,当销售强劲时,企业会新招聘一名员工;当销售不佳时,会解雇一名员工;当不再拥有任何员工时,企业也就“寿终正寝”了。这样一来,返回次数的分布就等于企业生命周期的分布,而且是一个幂律分布。大多数公司生命很短,只有很少的公司可以有很长的生命周期。
简单随机游走模型只在一个维度上进行。我们还可以对高维随机游走建模。二维随机游走从平面中的原点(0,0)开始,然后在每个周期中随机走向东、南、西、北。二维随机游走类似于在一张纸上绘制出来的一条弯弯曲曲的线,同时也满足递归性(recurrence)和无界性,有点儿类似于在你的起居室中随机搜索一只丢失的耳环时的路线。总是会回到起点。这种递归性使随机觅食成了蚂蚁的一个觅食策略。如果二维随机游走不是递归性的,那么蚂蚁就需要更复杂的内部地图或更强的信息踪迹才能找到它们的巢穴。但是在有三个维度的情况下,随机游走将不再满足递归性。在一个房间里到处飞的苍蝇和在空气中弹跳的分子都只会有限次地返回到它们的起点。
随机走动的应用
其中一个应用就是可以利用低维的随机游走的回到原点性来估计某个网络的规模。随机选择一个节点,然后沿着网络的边开始随机走动,并跟踪它回到原节点的频率。其回到初始节点的平均时间与网络的规模呈正相关。
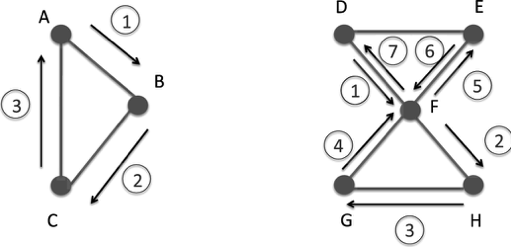
如上图两个网络,左图无论哪一点都可以3步回到原点,从D点开始则需要7步才能回到原点,可以看出右边的网络比较大。
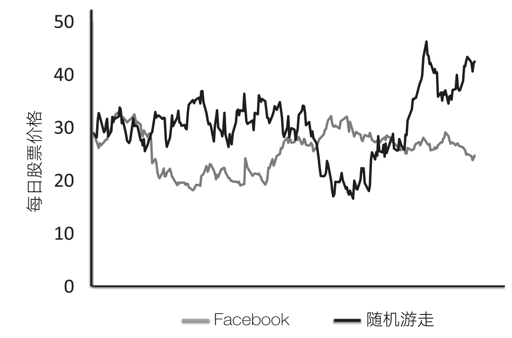
另一个随机走动的应用是在股票价格上。下图显示了Facebook在2012年5月18日首次公开发行后一年中的每日股票价格数据。Facebook公开发行时的价格为每股42美元。截至2012年6月1日,股票价格已经下跌到了28.89美元。一年后,价格进一步下降至24.63美元。下图还显示了另一个已经校准为具有类似变差的随机游走。
我们可以对Facebook的股价序列进行统计检验,以确定它是不是真的满足正态随机游走的假设。首先,价格应该以相同的概率上下波动,在这个序列所涵盖的249个交易日内,Facebook的股票价格在127天内是下跌的,占总交易日数的51%。其次,在随机游走中,增加的概率应该与前一周期的增加无关,Facebook的股票价格连续两天在同一方向上发生变化的时间只占总时间的54%。最后,持续出现在同一方向上的最长波动应该是8天,在这一年时间里,Facebook的股票价格曾连续10天上涨。因此,总的来说,我们不能否认Facebook的股票价格与随机走动一致的假设。
一些经济学家将这种随机走动思想进行了扩展,提出了有效市场假说(efficient market hypothesis)。这个假说指出,在任何时候,股票的价格都反映了所有的相关信息,未来的价格必定遵循随机走动。有效市场假说依赖于一个自相矛盾的逻辑。因为要确定准确的价格需要付出时间和精力,财务分析师必须收集数据并构建模型。如果价格真的是随机走动的,所有这类活动都将无法得到预期的回报。然而,如果真的没有任何人花费时间和精力去估计价格,那么价格就会变得不准确,也就意味着人行道上会铺满百元钞票。
简而言之,正如格罗斯曼和斯蒂格利茨悖论所强调的,如果投资者相信有效市场假说,他们就会停止分析,从而导致市场效率低下;而如果投资者认为市场效率低下,他们就会应用模型进行分析,从而提高市场效率。
小结
生活中的一些事情看起来有一定规律可循,但也可能只是随机走动。随机走动具有回归原点的特性,大概也可以解释“物极必反”这个成语。