模型思维(9)--熵:对不确定性建模
这一篇我们来讨论“熵”的概念。熵可以用来计算一个系统中的失序现象,即混乱程度。简单来说,一个事件的熵越高,其可能带来的惊喜越大,因为其结果是无序,不可预测的。熵是一个用来描述系统状态的函数,在控制论、概率论、天体物理、生命科学中等领域都有应用。这里我们研究其在信息中的定义和应用。
信息熵
熵可以度量与结果概率分布相关的不确定性。我们可以利用抛硬币来进行理解,对于抛硬币的结果,只有正反面两种可能,其概率都是1/2,其不确定性较小,无论怎么猜都有50%的概率回答正确。但如果抛三次硬币,其可能出现的序列就有8种,如果我们想猜对的难度就大大增加。
给定一个概率分布$(p_1, p_2, p_3, p_4 … P_N)$,其信息熵H等于:
$$H(p_1, p_2, p_3, p_4 … P_N) = - \sum ^N_{i=1} p_i log_2(p_i)$$
这里H的大小代表了其概率分布的情况,当H越大,说明不同结果的可能性越多。
我们可以从另一个角度思考这个数值,熵可以看作我们需要问几个是否的问题来确定结果。对于扔一次硬币的情况,其熵是1,所以我们问一个问题就知道其结果。对于扔三次硬币的情况,其熵是3,我们需要问三个是否的问题才可以知道其序列的情况。
熵的应用和最大熵
对于熵有这么一些特性:
- 最大化:对于所有的N,当$p_i = 1/N$ 时熵最大
- 零性:$H(1,0,0 …0) = 0$
- 可分解性:如果一个事件是由两个独立事件共同发生造成的那个$H(P) = H(P1) + H(P2)$
熵可以用来区分不同的时间序列的类型,分别是均衡、周期性、随机性和复杂性。
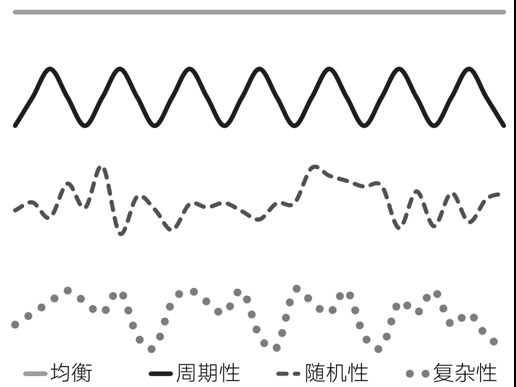
均衡数据没有不确定性,所以熵为0。周期性数据具有不随时间变化的熵,其结果比较低,因为是可以预测的。对于随机的数据,其熵最大。而复杂的数据其熵介于随机数据和周期性数据中间。虽然熵在两种极端情况下能够为我们给出明确的答案——均衡和随机性;但是这并不适用于周期性和复杂性的结果。在这些情况下,通常还必须善用我们的判断力。
当我们对于时间序列的熵进行分析时,我们可以先计算出不同子序列的熵。我们从时间长度1开始计算熵,之后计算长度2到n的序列复杂程度。如果熵增长到一定程度就不变了,那么说明可能是周期的数据类型。如果熵一直是最大的熵,那么可能是复杂的过程序列或是随机序列。
对于不同的条件下,得到的最大熵的分布是不同的。
- 均匀分布:给定范围[a,b],使熵最大化。
- 指数分布:给定均值$\mu$,使熵最大化。
- 正态分布:给定均值$\mu$和方差$\sigma^2$,使熵最大化。
在前面关于正态分布的介绍中,我们通过中心极限定理对于进行了解释。我们也可以利用熵对正态分布进行解释,如果一种突变能够最大化熵,并且假设平均规模和总离散度是固定的,那么规模的分布将会是正态的。关键不在于这种最大熵方法是不是提供了一个更好的解释,而在于给定约束下最大化熵必定会导致正态分布。
小结
熵可以用来衡量信息的不确定性,在接下来的文章中也会提供一些应用熵的思路。通过对熵的研究,可以加深我们对于世界的理解,知道其不确定性有多大。
一个系统中的熵的本质,不能简单地说好,也不能简单地说不好。我们想要多少熵,取决于具体情况。在制定税法时,我们可能需要一种均衡行为模型,并不希望有随机性。在规划城市时,我们可能会希望看到复杂性,均衡或者周期性都会显得过于平淡。我们希望一个城市充满生机活力,为偶然的相遇和互动提供无限机会。在这种情况下,更多的熵会更好,但是又不能太多。我们不喜欢随机性,随机性会使计划变得非常困难,并可能导致我们的认知能力崩溃。最理想的情况是,世界会产生适度的复杂性,以保证我们生活在一个有趣的时代。