模型思维(8)--广播模型、扩散模型和传染模型
这里我们将讨论三种传播模型,和目前世界正在经历的covid-19息息相关。这些模型同时也可以用来研究信息、技术、行为在人群中的传播,模型会将人群分为两部分,分别是知道的(感染的),不知道的(健康的),通过定义一些参数研究其中互相转换的关系。
广播模型
我们假定有一个固定人数的群体,其总人数是$N$。我们将$t$时刻知道这个信息的人看作$I_t$,除了这些知道信息的人以外,剩下的人都是可能获取信息的人,我们称作$S_t$。总人数 $N = S_t + I_t$。
$$ I_{t+1} = I_t + P_{broad} \times S_t$$
其中$P_{broad}$是广播概率,初始状态$I_0 = 0$且$S_0 = N$
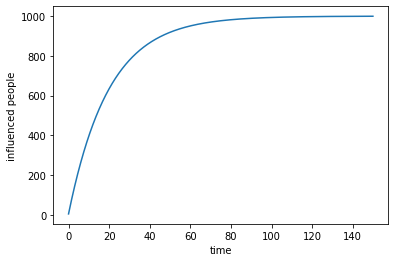
由上图可以看出当在初期时增长速度很快,到了后期增长速度越来越慢是因为大部分人已经知道了,在$S_t$会越来越小,如果广播概率不变自然增长的人数会很慢。广播模型刻画了思想、谣言、信息通过电视、广播、互联网传播的行为。这里的传播概率几乎不变,所以并不能很好的刻画人与人之间的传播。
扩散模型
很多传染病和信息是通过人人口耳相传的,所以我们需要扩散模型来考虑。事件的扩散在不同环境下是不同的,例如在城市中人们相遇的概率大大高于农村,非常吸引人的新闻的分享程度也比普通新闻高。在这里我们需要考虑到不同人的接触概率$P_{contact}$和分享概率$P_{sharing}$,我们定义扩散概率$P_{diffusion}$是这两个概率的乘积。
$$I_{t+1} = I_t + P_{diffusion} \times \frac{I_t}{N} S_t$$
与传播模型的区别在于这是S型曲线,在初期增长很慢,因为在人群中没有什么人知道这个信息,之后会快速增长因为知道信息的比例变大的,到了后期因为大家都知道这个信息了,所以增长速度又会放缓。
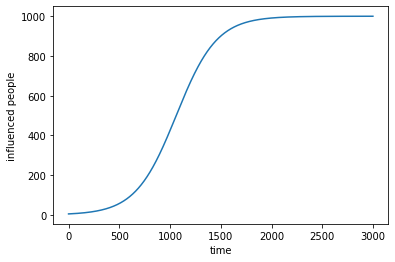
大多数消费品和信息都是通过广播和扩散传播的。而巴斯模型则将这两个过程组合在一起了。5巴斯模型中的差分方程等于广播模型和扩散模型中的差分方程之和。在巴斯模型中,扩散概率越大,采用曲线的S形就越显著。电视、收音机、汽车、电子计算机、电话机和手机的采用曲线形状都是R形和S形的组合。
$$I_{t+1} = I_t + P_{broad} \times S_t + P_{diffusion} \times \frac{I_t}{N} \times S_t$$
传染模型 SIR
当我们需要给传染病的传播建模时,我们需要考虑到得病的人会痊愈,与前面模型相比我们需要考虑治愈概率$P_{recover}$。
$$I_{t+1} = I_t +P_{contact} \times P_{spread} \times \frac{I_t}{N} \times S_t - P_{recover} I_t$$
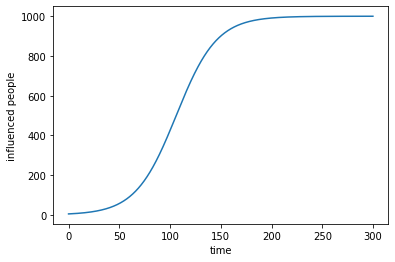
这里假定治愈的人不会再染病,所以出现到了顶点之后快速下降,因为后期的$S_t$会越来越小了。
SIR模型会产生一个临界点,就是所谓的基本再生数R0,也就是接触概率乘以扩散概率与痊愈概率之比。某种传染病,如果R0大于1,那么这种传染病就可以传遍整个人群,而R0小于1的传染病则趋于消失。在这个模型中,信息(或者,在这个例子中是传染病)并不一定会传播到整个相关人群。能不能做到这一点取决于R0的值。因此,像疾病控制中心这样的政府机构必须依据对R0的估计来指导政策制定。
$$R_0 = \frac{P_{spread} \times P_{contact}}{P_{recover}}$$
各种疾病的基本再生数$R_0$
| 麻疹 | 脊髓灰质炎 | 艾滋病 | 流感 | |
|---|---|---|---|---|
| R0 | 15 | 6 | 4 | 3 |
在没有疫苗的情况下,检疫是一个选择,但是成本很高。如果存在疫苗,那么疫苗接种可以预防传染病传播。即便做不到每个人都接种疫苗,也可以预防传染病传播。必须接种疫苗的人的比例,即疫苗接种阈值可以这么计算。假设V个人接种疫苗。我们需要让新的$R_0$小于1.
$$\frac{R_0}{N} (N-V) \leq 1$$
可以推出$V/N \geq \frac{R_0 - 1}{R_0}$。
小结
尽管SIR模型原本是用来分析传染病传播的,但是我们也可以将它应用于所有先通过扩散传播,然后趋于消失的社会现象,例如书的销售、歌曲的流行、舞步的风行,“热词”的传播、食谱和健身方法的流传等。在这些情形下,我们也可以估计接触概率、传播概率和“痊愈”概率,以及基本再生数R0。这个模型意味着,这些概率只要发生了微小的变化,就可以使R0移动到高于1的水平,从而造成成功与失败之间的天壤之别。